MetapopulationDaijiang LiLSU1 / 17

Announcements

Exam 1

2 / 17

Population dynamics so farExponential growth with unlimited resource
Logistic growth (Carry Capacity K)
Age structures
Closed population and dispersal

3 / 17

MetapopulationThe movement of individuals among sites can be potentially important to the persistence and survival of populations.Metapopulation: population of populations (Levins 1970); a group of several local populations linked by immigration and emigration4 / 17

Scaling populations to landscapes

No longer focus on number of individuals (i.e. population size); instead we focus on the population's persistence (i.e., local extinction or local persistence)
Shift to focus on regional and landscape level with many connected sites; we no longer focus on the persistence of any particular population; instead we try to understand the fraction of all population sites that are occupied

5 / 17

parking lot; does not care about a specific lot, but the proportion of opening/filled lots

Local vs regional extinction risk

local extinction: a single population extinct

regional extinct: all populations in a system extinct (metapopulation die out)

One population

$p_{e}$ : probability of local extinction, e.g. $p_{e} = 0.7$

probability of persistence = $1 - p_{e}$ , e.g., 0.3

6 / 17

Local vs regional extinction risk

local extinction: a single population extinct

regional extinct: all populations in a system extinct (metapopulation die out)

One population

$p_{e}$ : probability of local extinction, e.g. $p_{e} = 0.7$

probability of persistence = $1 - p_{e}$ , e.g., 0.3

Multiple (e.g., $n = 5$ ) population

probability of regional extinction = $(p_{e})^{n}$ = ${0.7}^{5}$ = 0.16807

probability of regional persistence = $1 - (p_{e})^{n}$ = $1 - {0.7}^{5}$ = 0.83193

6 / 17

Local vs regional extinction risk

local extinction: a single population extinct

regional extinct: all populations in a system extinct (metapopulation die out)

One population

$p_{e}$ : probability of local extinction, e.g. $p_{e} = 0.7$

probability of persistence = $1 - p_{e}$ , e.g., 0.3

Multiple (e.g., $n = 5$ ) population

probability of regional extinction = $(p_{e})^{n}$ = ${0.7}^{5}$ = 0.16807

probability of regional persistence = $1 - (p_{e})^{n}$ = $1 - {0.7}^{5}$ = 0.83193

Spread of the risk: a set of populations can persist for a surprisingly long time

6 / 17

Metapopulation models

Assumptions

a set of homogenous pathes
no spatial structure
no time lags: instantaneous response
constant colonization/immigration and extinction rates
regional occurrence affects local colonization and extinction rates
large number of patches

7 / 17

Parameter symbols in notes vs book

	Notes	Book
Fraction of sites occupied	$N$	$f$
Colonization rate	$c$	$p_{i}$
Extinction rate	$e$	$p_{e}$

$p_{i}$ : is approximately the proportion of open sites colonized per unit time

$p_{e}$ : the probability that a site becomes unoccupied per unit time

8 / 17

Metapopulation models

$\frac{d f}{d t} = I - E$

9 / 17

Metapopulation models

$\frac{d f}{d t} = I - E$

$I = p_{i} (1 - f)$

9 / 17

Metapopulation models

$\frac{d f}{d t} = I - E$

$I = p_{i} (1 - f)$

$E = p_{e} f$

9 / 17

Metapopulation models

$\frac{d f}{d t} = I - E$

$I = p_{i} (1 - f)$

$E = p_{e} f$

$\frac{d f}{d t} = p_{i} (1 - f) - p_{e} f$

9 / 17

Metapopulation models

$\frac{d f}{d t} = I - E$

$I = p_{i} (1 - f)$

$E = p_{e} f$

$\frac{d f}{d t} = p_{i} (1 - f) - p_{e} f$

The above equation will serve as a template for developing alternative metapopulation models.

9 / 17

The island-mainland model

The equation in the previous slide is the simplest model for our metapopulation with $p_{i}$ and $p_{e}$ as constants.

$p_{e}$ is a constant so that the probability of extinction is the same for each population and does not depend on the fraction of patches occupied
$p_{i}$ is constant implies a propagule rain, a continuous external source of migrants

10 / 17

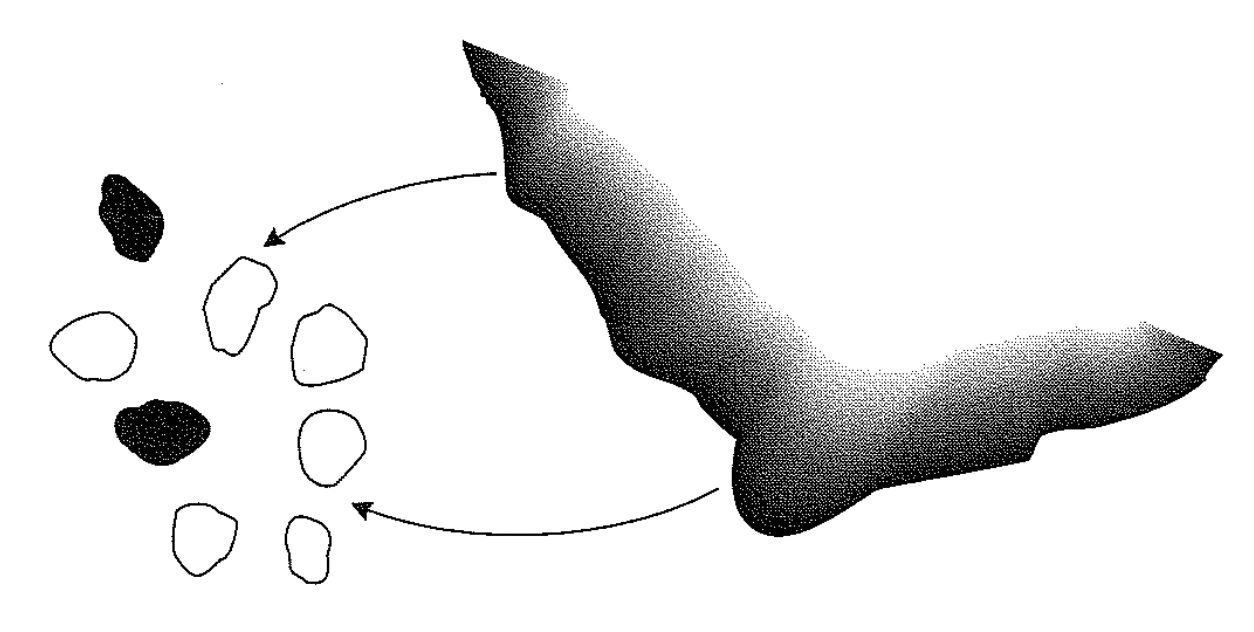
The island-mainland model

Equilibrium of f :

$\frac{d f}{d t} = 0 = p_{i} (1 - f) - p_{e} f$

$p_{i} f + p_{e} f = p_{i}$

$\hat{f} = \frac{p_{i}}{p_{i} + p_{e}}$

Note that even with large $p_{e}$ and small $p_{i}$ (it will always be >0 because of external sources), $f$ will still > 0, i.e. at least some of the sites in the metapopulation will be occupied.

11 / 17

Internal colonization (Levins model)

No propagule rain and the only source of propagules for the metapopulation is the set of occupied sites, i.e., internal colonization

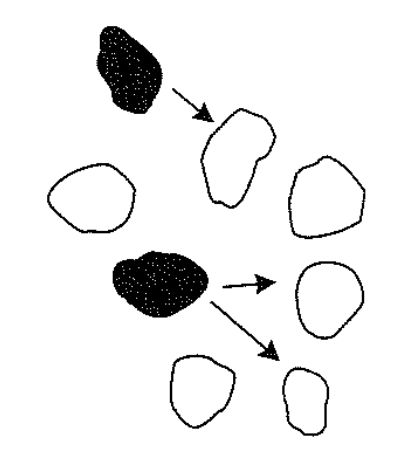
$\frac{d f}{d t} = p_{i} (1 - f) - p_{e} f$

$p_{i} = i f$

$\frac{d f}{d t} = i f (1 - f) - p_{e} f$

12 / 17

Internal colonization

Find Equilibrium

set the equation $\frac{d f}{d t} = i f (1 - f) - p_{e} f$ to 0
solve $f$

13 / 17

Internal colonization

Find Equilibrium

set the equation $\frac{d f}{d t} = i f (1 - f) - p_{e} f$ to 0
solve $f$

$i f (1 - f) = p_{e} f$

$p_{e} = i - i f$

$\hat{f} = \frac{i - p_{e}}{i} = 1 - \frac{p_{e}}{i}$

Note: if $\hat{f} \leq 0$ , metapopulation will go extinct because no external sources

13 / 17

The Rescue Effect

The above two models assumed that $p_{e}$ was a constant and was independent of $f$ .

$p_{e}$ might be affected by $f$ because with higher $f$ there would be more propagules that leave the site and may arrive at occupied sites to increase the local population size.

This increase in local population size $N$ is a rescue effect that may prevent the local population from extinct due to demographic and environmental stochastics.

14 / 17

The Rescue Effect

The above two models assumed that $p_{e}$ was a constant and was independent of $f$ .

$p_{e}$ might be affected by $f$ because with higher $f$ there would be more propagules that leave the site and may arrive at occupied sites to increase the local population size.

This increase in local population size $N$ is a rescue effect that may prevent the local population from extinct due to demographic and environmental stochastics.

$p_{e} = e (1 - f)$ $\frac{d f}{d t} = p_{i} (1 - f) - e f (1 - f)$

14 / 17

The Rescue Effect

The above two models assumed that $p_{e}$ was a constant and was independent of $f$ .

$p_{e}$ might be affected by $f$ because with higher $f$ there would be more propagules that leave the site and may arrive at occupied sites to increase the local population size.

This increase in local population size $N$ is a rescue effect that may prevent the local population from extinct due to demographic and environmental stochastics.

$p_{e} = e (1 - f)$ $\frac{d f}{d t} = p_{i} (1 - f) - e f (1 - f)$

$p_{i} = e f$

$\hat{f} = \frac{p_{i}}{e}$

14 / 17

Neutral Equilibrium

Internal colonization + Rescue effect

$\frac{d f}{d t} = i f (1 - f) - e f (1 - f)$

Equilibrium?? No simple solution!

$i > e$ , metapopulation grows until $f = 1$ (landscape saturation)
$i < e$ , metapopulation contracts until $f = 0$ (regional extinction)
$i = e$ , no change for $f$

15 / 17

Types of metapopulation

16 / 17

Four metapopulation models


Independent pepe
pepe mediated by rescue effect


External colonization (propagule rain)
dfdt=pi(1−f)−pefdfdt=pi(1−f)−pef
dfdt=pi(1−f)−ef(1−f)dfdt=pi(1−f)−ef(1−f)

Internal colonization
dfdt=if(1−f)−pefdfdt=if(1−f)−pef
dfdt=if(1−f)−ef(1−f)dfdt=if(1−f)−ef(1−f)

17 / 17

Four metapopulation models

	Independent $p_{e}$	$p_{e}$ mediated by rescue effect
External colonization (propagule rain)	$\frac{d f}{d t} = p_{i} (1 - f) - p_{e} f$	$\frac{d f}{d t} = p_{i} (1 - f) - e f (1 - f)$
Internal colonization	$\frac{d f}{d t} = i f (1 - f) - p_{e} f$	$\frac{d f}{d t} = i f (1 - f) - e f (1 - f)$

	Independent $p_{e}$	$p_{e}$ mediated by rescue effect
External colonization (propagule rain)	Island-mainland model	Rescue effect
Internal colonization	Levins model	Neutral equilibrium

17 / 17

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Metapopulation

Daijiang Li

LSU

Exam 1

Population dynamics so far

Metapopulation

The movement of individuals among sites can be potentially important to the persistence and survival of populations.

Metapopulation: population of populations (Levins 1970); a group of several local populations linked by immigration and emigration

Scaling populations to landscapes

Local vs regional extinction risk

One population

Local vs regional extinction risk

One population

Multiple (e.g., n=5n=5) population

Local vs regional extinction risk

One population

Multiple (e.g., n=5n=5) population

Metapopulation models

Assumptions

Parameter symbols in notes vs book

Metapopulation models

Metapopulation models

Metapopulation models

Metapopulation models

Metapopulation models

The above equation will serve as a template for developing alternative metapopulation models.

The island-mainland model

The island-mainland model

Note that even with large pepe and small pipi (it will always be >0 because of external sources), ff will still > 0, i.e. at least some of the sites in the metapopulation will be occupied.

Internal colonization (Levins model)

Internal colonization

Find Equilibrium

Internal colonization

Find Equilibrium

The Rescue Effect

The Rescue Effect

The Rescue Effect

Neutral Equilibrium

Internal colonization + Rescue effect

Equilibrium?? No simple solution!

Types of metapopulation

Four metapopulation models

Four metapopulation models

Exam 1

Help

Multiple (e.g., $n = 5$ ) population

Multiple (e.g., $n = 5$ ) population

Note that even with large $p_{e}$ and small $p_{i}$ (it will always be >0 because of external sources), $f$ will still > 0, i.e. at least some of the sites in the metapopulation will be occupied.